こんにちは!makoto(@Makoto_beginner)です。
おやおや、本日も何か会話が聞こえてくるぞ


ということで、本日は分散投資の威力について解説することにする。
1、分散投資とは?
「分散投資」とは、複数の資産に投資をすること
である。今回の例で言えば、「マタタビ商事」と「カツオ武士」の二つの会社の株を買えば分散投資になる。
また、今回は「会社別」で分散投資を行なったが他にも「日本の会社とアメリカの会社の株」のように国別に分散したり「鉄道業界と自動車業界」のように業種別で分散するなど様々な分散方法がある。
基本的に投資においては分散投資が鉄則となっている。その理由としては、一つの資産に全財産をつぎ込んでしまうとその資産がダメになった場合に一気に資産を失う可能性があるためだ。
とは言えど、分散投資をしても疑問猫の想像するようなグラフであれば、リターンを求めればその分リスクは増えてしまう。
だからこそ、疑問猫は一番リスクの少ない会社の株をすべての資金をつぎ込んで購入しようとしているが一体何がダメなのか?
実は、疑問猫の想像する図が間違っているのだ。
2、分散投資の真の威力
実は、理論上は分散投資を行えばすべての資金をつぎ込んで「マタタビ商事」の株を購入するよりも「リスクを減らしリターンを多くすること」が可能なのである。
一体どう言うことなのだろうか。
リスク・リターン平面とは?
疑問猫が想像していたこのグラフは「リスク・リターン平面」と呼ばれている。
(↓こんなやつ)
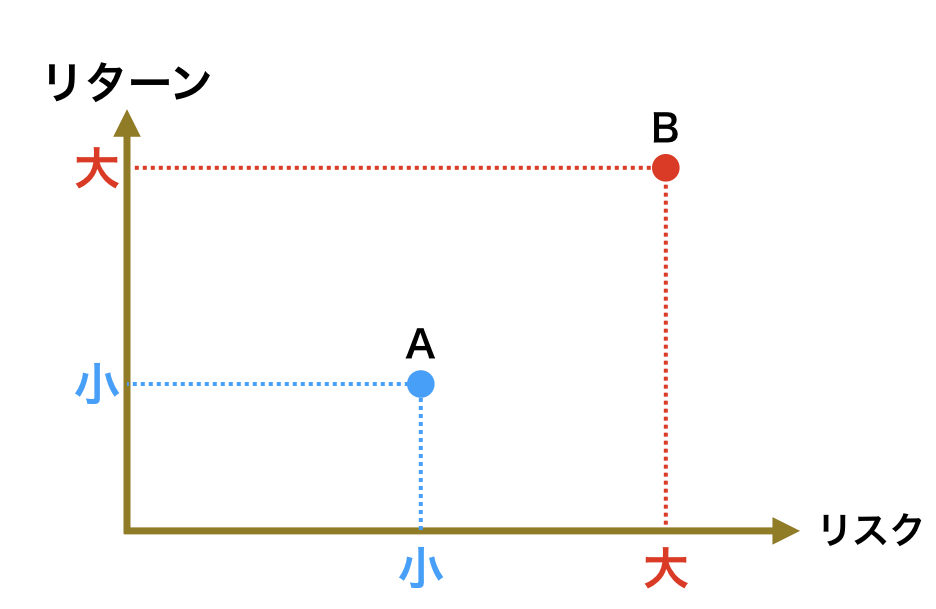
この図を使用することで、リスクとリターンの関係性が点の位置で視覚的に理解できる。
ここで、リターンは少ないがリスクも少ない資産Aと、リターンは大きいがリスクも大きい資産Bを考える。
資産Aと資産Bの保有比率を変えていくと・・・?
資産Aと資産Bを保有する比率をA:Bで表すことにする。そして、A:B = 10:0の時(つまり分散投資をせずにすべての資金をAに投資した場合)は図Aの位置に点がプロットされる。次に、A:B = 0:10の時(分散投資をせずにすべての資金をBに投資した場合)はBの位置に点がプロットされる。
では、この資産AとBを保有する比率を連続的に変化させると一体どんな線を描くのだろうか?
実は以下の図でオレンジで示した線のようになる。
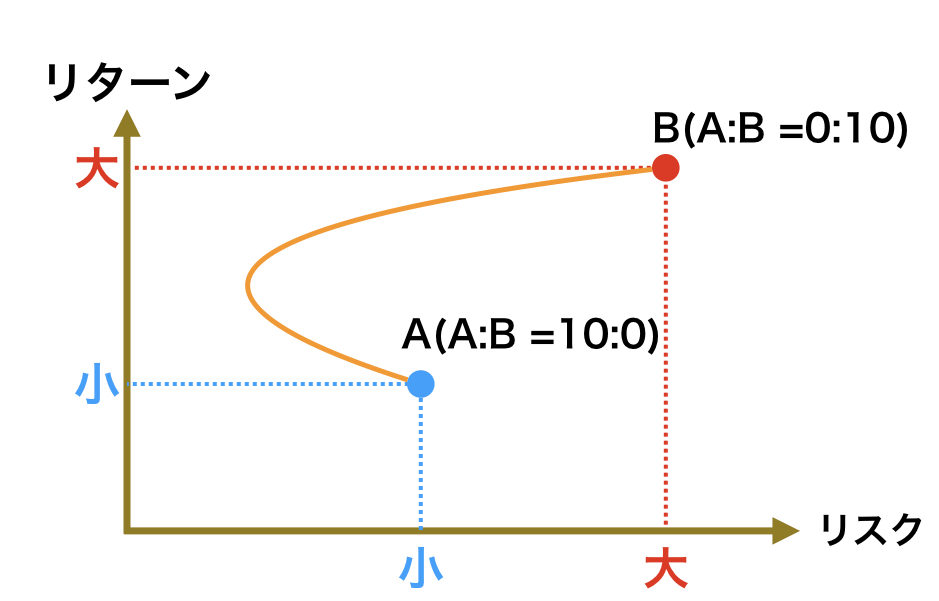
この図を見てピンとくるだろうか。わからない人は以下の図の点Cを見て欲しい。
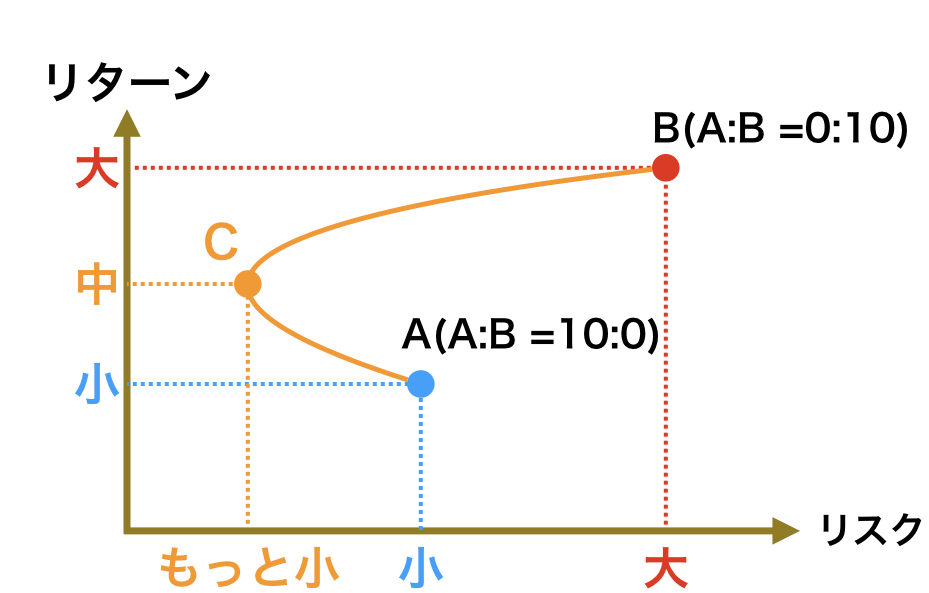
つまりどういうことか説明すると、資産Aと資産Bに分散投資をすることにより、資産Aのみに投資するよりもリスクを減らしつつリターンを大きくすることができるのである。
つまり、疑問猫はリスクを最小限にするために全額をAに投資しようとしていたが、実はリスクをもっと減らしつつリターンを大きくする方法があって、実はそれが分散投資だったというわけである。
これこそが分散投資の真の威力なのである。
また、分散投資を行うための資産の組み合わせのことをポートフォリオという。
3、なぜこんな曲線を描くのか?
ここからは少し難しい話になるので、興味がなければ4項まで飛ばしてもらって構わない。しかし、読者の中にはなぜこのような曲線を描くのか気になる方もいると思うので詳しく解説を行う。
リスクをどうやって評価するか?
そもそも、リスク・リターン平面の中でリスクをどうやって評価しているのか気にならなかっただろうか?
答えを言うと、将来期待されるリターンのばらつき具合を標準偏差σで表したものをリスクとして用いた。
一般的にリスクというと、結果に対して負の影響を与える要素であるとイメージされているが、実はファイナンスでいうリスクとは将来想定される結果のバラツキのことを指す。
つまり、自分の持っている株が急落するのもリスクだし、逆に急上昇するのもリスクということだ。
そして、数学の世界にはバラツキを表す指標として標準偏差σがあるので、リスク・リターン平面ではリスクを「リターンのばらつき具合を示す標準偏差σ」で表したのだ。
リスク(標準偏差σ)を実際に計算してみる
では、具体的なイメージができるように実際に標準偏差σを求めてみることにする。
以下に、ある会社の株式を購入した場合の、5年間のリターン率を示した表がある。
[table id=3 /]
ここで年間リターン率の平均値を計算すると、$\frac{(5+10-10-5+5)}{5}$ = 1%となる。
そして、各年のリターン率から平均リターンを引くことで平均リターンとの差を求める。そして、その値の二乗をとったものが分散となる。
標準偏差は、すべての分散を足した後に項の数-1で割り、そのルートをとることで求められる。
そのため、この例だとこのような式になる。
$σ^2 = \frac{(4)^2+(9)^2+(-11)^2+(-6)^2+(4)^2}{5-1}=67.5$
σ =$\sqrt{67.5}=8.21$
今回は標準偏差σは8.21となった。
そして、この数値が小さければ小さいほど将来の期待するリターンが安定していることになるのでリスクが小さいと考える。
逆にこの数値が大きければ大きいほど将来期待するリターンが大きくブレる事を意味するのでリスクが大きいと考える。
二資産を所有した時のリスク(標準偏差σ)はどうなる?
今考えたいのは2つの資産を保有し、保有比率を変化させた時にどのような線形となるかだ。
では、二つの資産を保有した時の標準偏差がどうなるかを求めることにする。
資産AとBのそれぞれにおいて、
標準偏差 :$σ_{1},σ_{2}$
保有する割合 :$w_{1},w_{2}$
標準偏差の相関係数 : $ρ_{12}$
とし、これらを組み合わせたポートフォリオの標準偏差をσとする。
すると、標準偏差の合成は以下の式で表される。
$σ$=$\sqrt{w_{1}^2σ_{1}^2 + w_{2}^2σ_{2}^2 + 2w_{1}w_{2}ρ_{12}σ_{1}σ_{2}}$
そして、$w_{1}+w_{2}=1$(保有割合を足すと必ず1となる)なので、
これを先ほどの式に代入すると以下の式を得る。
$σ$=$\sqrt{(σ_{1}^2 + σ_{2}^2-2σ_{12})w_{1}^2-2(σ_{2}^2-σ_{12}^2)w_{1}+ σ_{2}^2}$
この式は$σ$に対する$w_{1}$の二次方程式となっていることがわかるため、リスク$σ$に対して資産保有比率$w_{1}$を変化させていくと左方向に窪んだ形の線型となる。
4、投資対象をもっと分散させるとどうなる?
先ほどの例では2つの資産に分散投資を行なった場合を考えたが、実際はもっと多くの資産に分散を行う。すると、ポートフォリオのリターンとリスクは、先ほどと違い線ではなく面を構成する。以下図の青線部分がその面になる。

効率的フロンティアとは?
では、ポートフォリオCとC’が存在しそのリスクとリターンを、リスク・リターン平面上にとったものが上図だとすると、皆さんならCとC’のどちらのポートフォリオを選択するだろうか。
私であれば、間違いなくCのポートフォリオを選択するだろう。何故ならばCとC’はリターンが同じであるが、Cの方がリスクが小さいからだ。
この例からもわかるとおり、この面を構成している境界線(図中の緑線部分)部分こそ、リスクに対して最も多くのリターンを得ることができる最適な組み合わせの集合体であることがわかる。
この部分のことを効率的フロンティアと呼ぶ。
最小分散とは?
また、点C部分はどのポートフォリオよりもリスクを最小にすることができる点である。
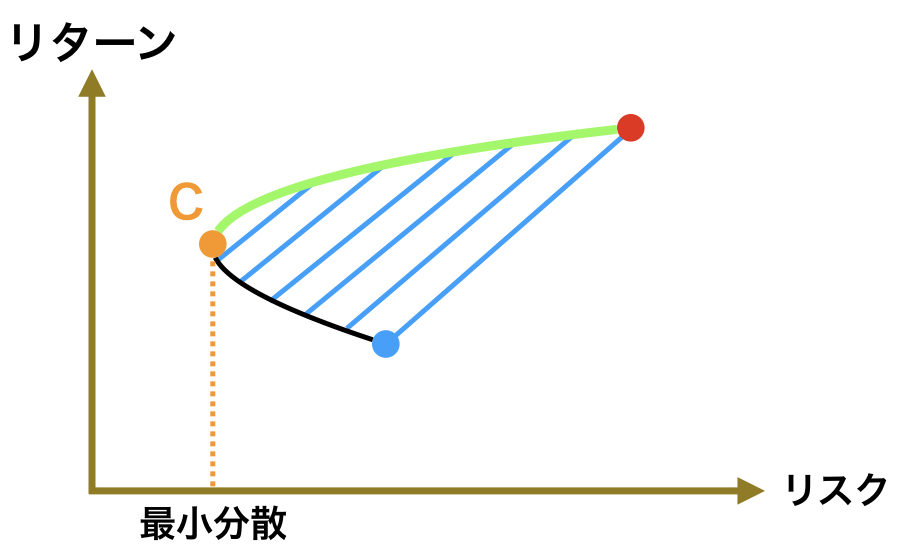
この点Cのように、リターンを考慮せずにリスクが最小となるように投資を行う方法を最小分散投資という。
(ちなみに分散とは標準偏差σを二乗した値のこと。つまり、最小分散とはσ(リスク)が最も小さいことを示しているのと同じである)
5、まとめ
1、「分散投資」とは複数の資産に投資をすること
2、「分散投資」によりリスクを減らしリターンを増やすことができる
3、分散投資を行うための資産の組み合わせのことをポートフォリオという
4、ファイナンスでいうリスクとは将来想定される結果のバラツキのことを指す
5、リスクに対して最も多くのリターンを得ることができる最適な組み合わせの集合体のことを効率的フロンティアと呼ぶ
6、リスクが最小となるように投資を行う方法を最小分散投資という
※免責事項※
当サイトにおける記事内容は一般的に入手可能な情報に基づいて管理人が解釈した上で作成しています。よって、記事内で発信していることは全て個人的な見解であり『株式およびそれに準ずる金融商品、資産など』の購入、売却等、投資を勧誘するものではありません。
また、それらの内容について当サイトがいかなる保証を行うものでもありません。
そのため本記事に基づいて投資を行い損失が発生した場合にも当サイトは一切の責任を負いません。
投資に関する決定は、ユーザーご自身のご判断において行われるようお願いいたします。
本記事を気に入っていただけたらブックマークお願いします!また、ツイッターもやってるのでフォローよろしくお願いいたします!
Twitter : makoto(@Makoto_beginner)
また、記事中で不明なことや間違い等ありましたら以下のコメント欄からコメントいただけると幸いです。
皆様のコメントをもとにどこよりもわかりやすいブログを目指していきます。