こんにちは！makoto(@Makoto_beginner)です。今回は投資と関係がありそうでないような記事を書こうと思う。
興味を持ってくれる人は、とことん興味を持って読んでくれると思っているので是非読んでみてほしい！
記事としては、「複利」について解説した前回の記事の続きになるのでそちらもぜひ！
１、「複利」の考え方に対しての違和感
前回の記事で「複利」の考え方について解説したが、私が初めて複利について学んだ時、少々違和感を感じた。
私が気になったのは「銀行の利子はいつの時点でつくのだろうか」ということである。
「1年に1度？毎月？それとも毎秒？」なぜこんな事が気になったのか、前回の図を用いて説明する。
この図は、元本100万円で年利10%の利子がつく場合、複利では5年後にどうなるかを示したグラフである。
ここで、私と同じ違和感を感じる人がいないだろうか。「預け始めから1年」経つまでをみてほしい。
そう、この期間は単利で計算されているのだ。
どういうことかというと、本来であれば預け始めから1年後までの間にもどんどん利子がついているはずなので、本当に複利運用されているのであれば1年後の利子が元本100万×10%=10万円となるはずがない。
もう少し詳しく説明するために、次にこんな例を考えてみよう。
２、年利100%の預金で最大リターンを得る方法とは？
ここでは架空の設定として、年利100%の銀行預金があるとする。元本を1とすると、1年後には1+1=2になっているので、資産の増加をグラフに表すとこうなる。
ここで、この銀行預金で得ることのできる最大リターンは元本の何倍かという問題を考えてみよう。
「いやいや、年利100%の預金ならリターンは+100%だから最大2倍でしょ？」と思う方もいると思うが、実はそうではない。
半年後に一度預金を引き出して再度預けるとする。すると、こんな事が起こる。
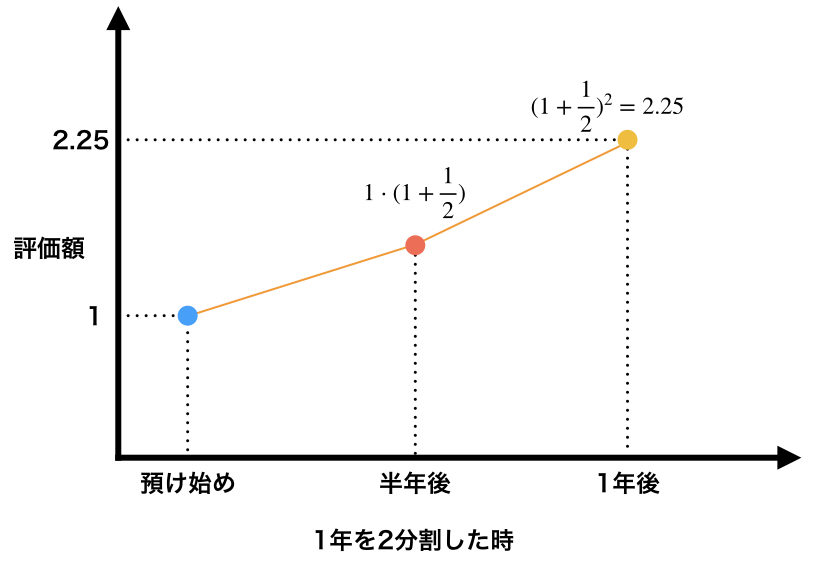
半年後は利率100%のうち半分が利子としてついているので、引き出す際の額は、$1\cdot(1+\frac{1}{2})$で表せる。
そして、それを元本として再度預けるため、最終的な額は$(1+\frac{1}{2})^{2}$となる。
よくわからなかったら以下の画像を見てもらえばなんとなくイメージできると思う。
半年後の額は、元本1に対し（100％＋利率の半分($\frac{1}{2}$)）を掛けたものになる。その半年後の額はその額$1\cdot(1+\frac{1}{2})$を元本にするため、先ほど1だったところにその値を代入すると、最終的な額が求められる。
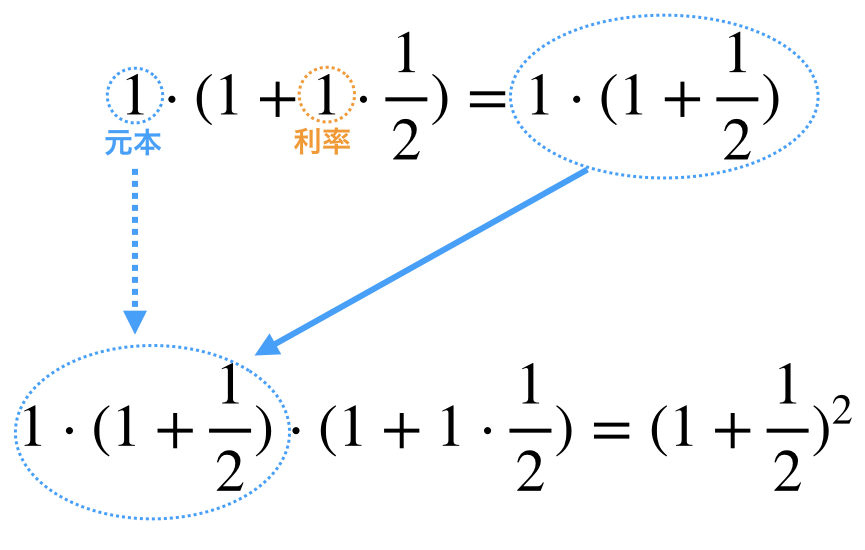
そして、$(1+\frac{1}{2})^{2}=2.25$であるため、そのまま預けている場合に比べ、半年後に一度引き出して再度預け直す方がリターンを大きくできるのだ。
では次に、1年を4分割にしてみたらどうだろうか。
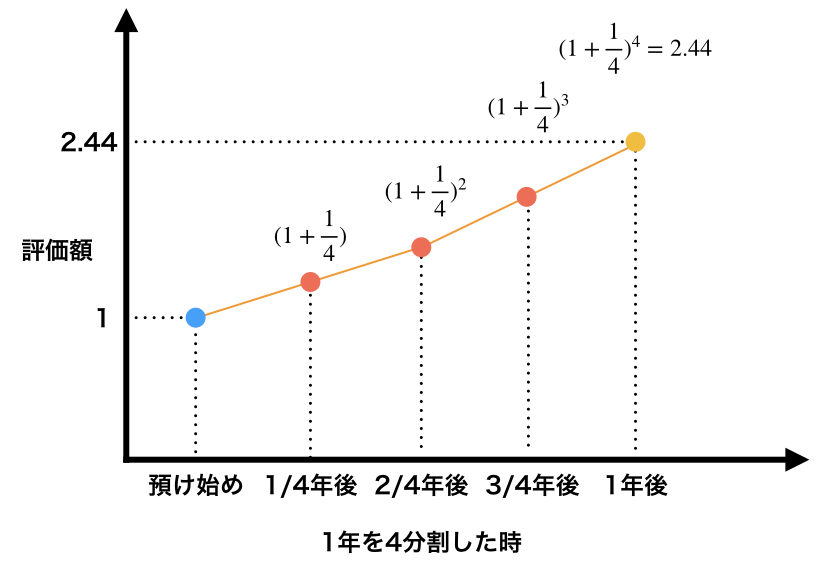
これも同様に計算すると最終的には2.44となり先ほどの２分割した時よりもリターンが増えている。
この例から、1年を分割すれば分割するほどリターンが増えそうな気がするのがわかる。
では、1年をn分割した時の式はどうなるのだろうか。以下の画像を見ればすぐにわかる。
そして、分割数nを大きくすればするほどリターンが増えそうな気がするので、極限をとりnを無限に大きくしていくと、こんな数になる。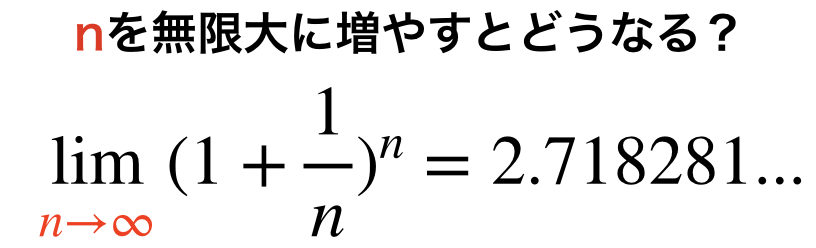 
そう、この数字を見た事があるかもしれないがこの数はネイピア数eと呼ばれる特別な数である。円周率πと同様に、数がずっと続いていく無理数である。
つまり、利率100%の銀行預金があれば最大で元本の2.718…倍にする事ができるというのがこの問題の答えとなる。
つまり、私が複利を最初に学んだ時に抱いた疑問「利子はいつになったらつくのか？」という疑問はこの連続複利の考え方を元に抱いた疑問であった。もし毎日、いや毎秒、いや微小時間で利子がつくのであればこの様な事が可能になってしまうのだ。
３、ネイピア数eとは？
ところで、ここで出てきたネイピア数eとは何者なのだろうか。
実は、今回の連続複利以外にもこのネイピア数eは現れる。
１）自然対数の底である
高校数学で対数$\log$というものを学んだと思う。具体例を挙げると、$\log_2 8$を解く場合、これは$log$の右下についている数字、ここでは2の何乗が8になりますか？という意味であり$2^{3}=8$ であるため$\log_2 8 = 3$が答えとなる。そして、ここでいう2のことを底というのだが、この底がネイピア数eである対数を自然対数という。
この自然対数は$\log_e$とは表記されず、多くの場合は$\ln$と表現される。
「そんなの見たことはない！」という方は、ぜひスマホの電卓を見てみてほしい。少なくとも私のiPhoneの電卓にはこの$\ln$がいる。ちなみにネイピア数eもいる。
自然対数と言われるくらいなので、様々な事象の計算の際に自然対数は使われている。不思議ですね。
2）席替えで席が変わらない確率・プレゼント交換で自分のプレゼントを受け取る確率
実はこんなとこにもネイピア数eが登場する。
席替えを実施して席が変わらない確率やプレゼント交換で自分のプレゼントを自分が受け取る確率は、37%に収束すると言われている。
実はこれもネイピア数eの逆数、つまり$\frac{1}{e}$なのである。非常に不思議ですね。
3）カタツムリやアンモナイトの殻、台風、牛や羊の角
ネイピア数は自然界にもたくさん存在している。例えば、カタツムリやアンモナイトの殻、台風の形、牛や羊の角は螺旋を描いているが、この螺旋は対数螺旋と呼ばれネイピア数eを使って表される。
極座標表示（r, θ) を用いて$r＝ae^{b}{θ}$
a,bはともに実数。
他にも、鳥が獲物を捕る際に対数螺旋を描きながら飛行することも確認されているらしい。もはや不気味ですね。
他にも世界一美しい式と言われているオイラーの公式にもeが登場する。
４、まとめ
ネイピア数eはどこにでも現れる特別な数字
今回は、連続複利の話をしたが実はネイピア数eの神秘について語りたかっただけである。
一見規則性がない様なものであっても実はこの様に何かの式や値に縛られているのかもしれない。しかも、たった一つの値によって。。。
ネイピア数eは身の回りの様々なとこに現れる不思議な数である。
「ネイピア数なんてそんな数知らない！」というあなたの身の回りにもeが潜んでいるかもしれません・・・
ほら、あなたの後ろに・・・！（終）
本記事を気に入っていただけたらブックマークお願いします！また、ツイッターもやってるのでフォローよろしくお願いいたします！
Twitter : makoto(@Makoto_beginner)
また、記事中で不明なことや間違い等ありましたら以下のコメント欄からコメントいただけると幸いです。
皆様のコメントをもとにどこよりもわかりやすいブログを目指していきます。
